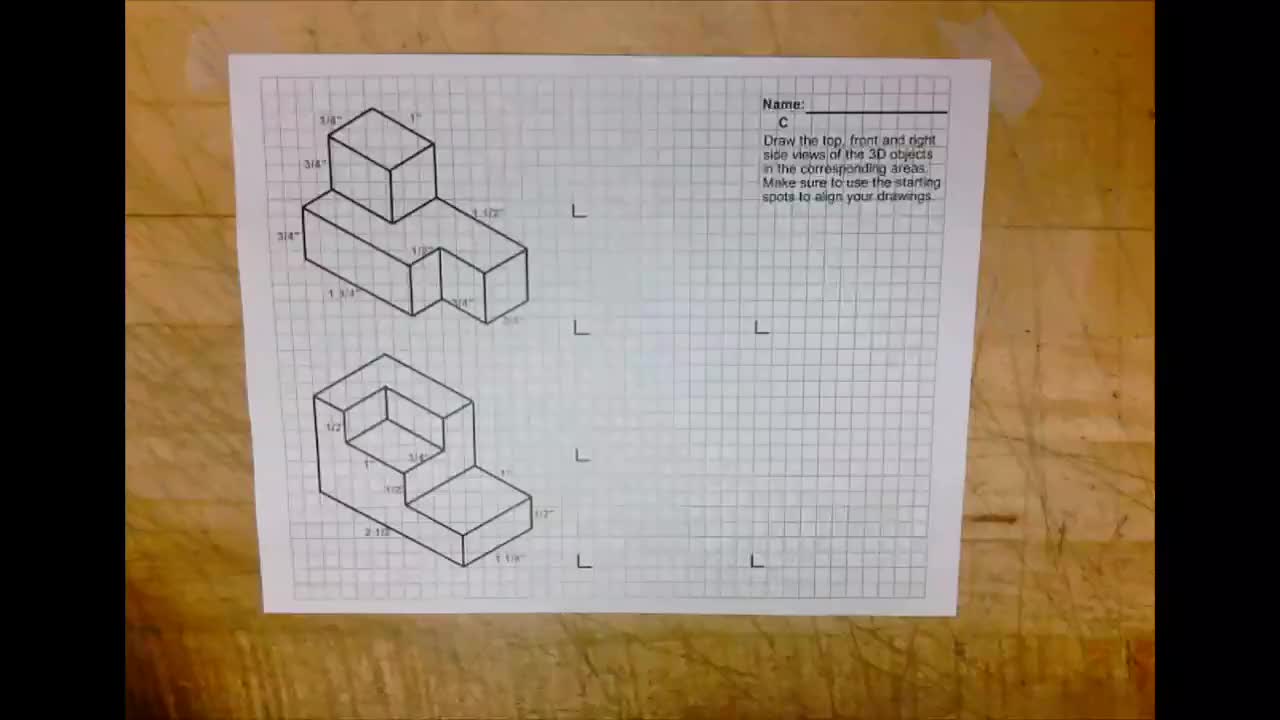
Unit 7 Geometry Exam Review

Hi everybody, welcome to our unit 7 review on dilation and similarity. Click reminder our test is going to be next Wednesday that's fourth so hopefully this helps you study. All right, let's get started. The first question says the segment AB has endpoints at a negative two comma 5 and B two comma three, which of the following is the length of a prime B prime, which is the image of AB after a dilation by a factor of 6 that's a terrible underline. Dilation by a factor of 6 centered at the origin. Okay, so what do we know about dilations? We know that dilations change size, but it does not change the actual shape of an object. So if we're dilating a line about the origin, there are two ways we can do this, okay? We can always take these endpoints and multiply them all the X's otherwise by 6, and then find the length. The other thing you could do is find the length of the original, and then multiply whatever that length is by 6 later on. So I think I'm going to do that one. I'm going to find the length of the original. So remember our distance formula is big square root. X two minus X one squared plus Y two minus Y one squared. Again, these can be wise, these can be X's here. It really doesn't make a difference. All right, and now let's just plug inappropriately. We'll call this X one, Y one. We'll call this X two Y two. All right, and all we got to do is plug in. So we have, again, big square root. X two is two minus X one is negative two. Squared, be careful of your symbols here. And we have Y two is three -5 squared. That's going to give us four squared, which is 16. Plus negative two squared, which is four. So we get radical 20. Now look at all our answers. Our answer is our own simplified radical form. Okay? So I'm going to simplify this radical. Red 20. Well, I know the largest perfect square that divides 20 is four. So I'm going to break this up into rad four times red 5. Okay, because four times 5 is 20. And now the square root of four is two, and we keep the rat font. Now this is the length of AB. Remember, we have a scale factor of 6 here, so just multiply this whole thing by 6. When you multiply by 6, all you have to do is multiply the two in the 6 and you get 12 red 5. You leave what's under the radical. So 12 rad 5 is our final answer here. All right, moving on to number two. In the diagram, it is known that EF is parallel to GH, so let me just mark that off quickly. Which of the following ratios would equal that dilation scale factor. So I want to figure out the scale factor needed to map GH onto EF. Now the order in which they write that is important, right? We're going from GH to EF. Okay? So we're getting smaller here. That's really important. Using a center point of D all right, so scale factor, we know we have to do new over old. Okay? And we know it's getting smaller because we're going from GH to EF. So let's see. If we do the proportion, GH divided by EF that really does is no good, right? Because GH is the longer side. We want to get smaller. That's not new over all. That's actually old. Over new. So that's no good. Okay? DF over DH. So it's a DF is this length DH. So let me highlight it. DF is this length while DH is the whole thing. This is actually new over old, right? You started with DH, because again, we started with GH as our line segment. This became DF. All right, so that's new over old. Your answer is number two. So read carefully, it's not always a bigger side over the smaller side. You have to identify where we're going. Okay, number three, in a diagram we have F prime E prime G prime. That's this angle right here. It's the image of angle FE G after dilation by a scale factor of 1.5, centered at point D if the measure of angle G is 30, I'm just going to write that down quickly. Then which of the following is a measure of its image, angle F prime E prime G prime. So we want to know this angle right there, okay? This is an easy question, guys. All right, don't fall into the trap and multiply 30 by 1.5. Remember, when we dilate, we only change the length of these line segments here, okay? So size changes the shape is not angles are preserved. So I'm just going to write a little note here. In dilations, or maybe with dilations, angles are preserved. So the angle is going to stay the same. It's number three. Don't fall into the trap and multiply it by 1.5 and get 45. Okay, next up, in the following diagram, BC is parallel to DE, so again, we have parallel. Really, the reason they tell us that guys is to tell us that these two triangles are similar, all right? We've seen this picture many, many times in class, right? If these two are parallel, we got some corresponding angles right here. And here, that's enough to have angle angle. But I digress. Let's see, a, B is 21. BD is 7, BC is 15. Then which of the following is the length of DE? Okay, so this is the picture that people always want to use side splitter theorem on, right? But we can't use side splitter here, okay guys, we can only use size blitter if this was 15 and this was X, right? There are cross from each other. When they're lengths given or the lengths we want to find are on the parallels, we can no longer use side splitter. Now, this is not the right answer, so don't write it down. People want to do this. 21 over 15, because those two go together equals what, 7 over X but look, 21 is the length of this small triangle. That's fine. 15 is the bottom of that small triangle also fine. But 7 is just BD. That's not part of the big triangle, right? Whereas X is the whole length of the big triangle. So we can't set this up, okay? But we can set up, we're going to highlight this. Using that small triangle again, and then using the big triangle. Okay? So we can set this up. 21 over 15. That's fine. Equals now we just need the length of the entire bottom. 28. Over X guys, we need the entire bottom because X is the entire right hand side of the triangle. So this is the way we can set it up. You also could have just found what the scale factor was and from 21 to 28. And then multiply 15 by that same number, that would work. But let's see if we get 21 equals, I'm sorry, 21 X sorry about that equals that gives us 420 divide by 21 and X is 20. Okay, and it's choice number three. Next up, number 5, triangle points and in R located on sides MP and QP with NR drawing. Okay, so they just connected two points. They didn't say that those are midpoints. They didn't say anything special about them. They're just two points. Which set of measurements below would justify that MP Q is similar to NPR. All right, so we want to justify that dissimilar. That means that these side lengths need to be in proportion. All right, so let's check it out. PN is ten p.m. is the whole thing. It's 12, okay? PR's 18. PQ is 20. So we have to see if those are in proportion with one another, all right? So the easiest thing to do is just do 12 over ten. Find out if that's equal to 20 over 18. Okay? This gives you 1.2. This gives you some number that's not 1.2. Okay, I don't have my calculator next to me right now, but this is not 1.2. So that answer is incorrect. And you can go ahead and try the rest, all right? You can try every single one. Because each one then gives you PN p.m. PR PQ. So I'm just going to do the rest of them pretty quickly, okay? If I have PN and p.m., that means it's got multiplied by two, right? PR would have to get multiplied by two, but clearly it did not to get 15. So they're not in proportion. PN to p.m. is 12 to 16 if I do this quickly 16 over 12. If I simplify that, that's just four over three, okay? 25 over 15, simplified is 5 over three. So that's no good as well. So it has to be answer choice number four. All right, but let's just be sure. 9 over 6 is three halves. 12 over 8 simplified is also three halves. So those are in proportion, that's the right answer. All right, number 6, and the diagram below. E and F lie on segments DG and DH. Okay, again, these are midpoints. There's nothing special about them. They just picked two points. Which of the following statements would not be enough to justify DEF is similar to DG H okay, so if we want to justify that two pieces are similar, remember what we need to show. Okay? We need to show either angle angle, side angle side, or side side side. Okay, and remember for similarity, these are not congruent sides, their sides in proportion. So let's see, if EF is parallel to GH, okay? This is the picture we've seen a million times, right? That means we have corresponding angles here. And here, the triangles would be similar by angle angle. So I'm just going to make myself a little note here. That would be angle angle, okay? DEF, this angle is congruent to angle DH G all right? Well, that might not be in the spot that you would want it to be, okay? But angle D isn't that just a reflexive angle for both triangles, okay? So technically they have angle angle. It might be drawing a little bit funkier than you'd think, but it still works. Next one, E and F are midpoints of size DG and DH. All right, so if these are midpoints, that means these two are congruent. And those two are congruent. Okay? Well, if these two are the same and so are these, then that means that these sides are in proportion, right? DE over DF is the same thing as EG over FH. They have to be, right? Because DF and FH are exactly the same thing. And these are exactly the same thing. So I could really just replace them with each other if I wanted to. And angle D is reflexive. This is side angle side. And sorry, I should angle angle here. Okay. Last but not least, we have answer choice four. And that says that DE is in proportion with DG. So DE is in proportion with this entire side right here. EF is in proportion with the entire bottom. Okay? That does not prove these two triangles are congruent. All right, guys. This would, I'm sorry, not congruent similar. This would be a byproduct of the two triangles being similar. But it doesn't necessarily show that they are similar to begin with. Okay? So this is your answer for what does not justify them. All right, moving on to number 7. Okay. In the diagram of the right triangle EFG point H and K are located on sites EG and FG such that HK's perpendicular to the side EG as shown, which of the following equations must be true based on this diagram assuming that those two triangles are congruent. Okay, be careful. This picture is not the same as this picture, right? Student for things. This is not an altitude because it doesn't come from the opposite vertex. So don't get those two things confused, all right? All they're saying is this big triangle EFG is similar to the small triangle. So what I did is I pulled these two triangles apart, okay? I took the big triangle. I rewrote it. This is E, F, G okay, without pulling them apart it's very hard to do. Okay? Now I can see why you wouldn't pull them apart if you thought we were doing the tree. Thing that we do, okay? But it's not the trees because we don't have an altitude. And then you take your small triangle. Now you have to be careful when you take your small triangle. You have to put things in the right place. If your right angle is on the bottom left here, you need your right angle to be on the bottom left here. And that is where K is. Okay? So basically just taking this and flipping it. So G doesn't move, but H is going to come up here. So those are the pieces that correspond to each other. You also just could have looked at what they wrote. E corresponds to H, F to K, G to G that would have been another way to do it. All right? So let's see. EG over HG, so that's the hypotenuse of both so far so good. Equals EF over KG. That doesn't work, right? Because EF is to the left cages on the bottom. Those are not corresponding parts. That's out. Okay, number two, we have FG is in proportion with KG. We have EF in proportion with HK. That's good, right? We have side angle side, so we're all good here. The sides correspond to each other. We're ready to roll. Okay, and actually the fact that it's side angle side doesn't matter. The important part is that they use the corresponding sides. Next up, segment AB has endpoints at a three comma 7 and B 23 comma negative three. All right, here's one of these partitioning questions. If point C is located on AB, such that your ratio is that, which of the following must be the coordinates of C all right, so here's what I'm going to do guys. I'm just going to do the formula. I know a lot of you really like to graph it and that's awesome. I like to grant it as well. Just I don't have graph paper on the computer and getting to 23 is tough to do. But remember, we're going to supply you with graph paper on the test so you have plenty of room to do this if you want. We also wouldn't use the numbers biggest 23 on the test. But let's try this out. So remember the formula I said was X equals X one plus R which R is the entire ratio. Times X two minus X one. Now what's important here is that since a is first, we only are allowed to use a so this is my X one a, this is my X two at B so plug in X equals three plus now your rate or ratio a corresponds to the three here. In total, there's 5 pieces. So AC is really three fifths of this whole thing. So three fifths is what you want. And then you're going to do negative three minus. I'm sorry, that's the Y value, oops. 23. Minus three. Okay, so you get X equals three plus three over 5 times 20. Okay, you can put that whole thing in your calculator right there and you will get X is 15. Okay. So let me move this out of the way here. Next up is the Y's, Y's are the same formula just literally with wise instead of X's. So Y is equal to Y one plus R times Y two minus Y one. Again, a has to be Y one B has to be Y two because that's the order in which they wrote it. So you have Y equals 7 plus your rate stays the same dives were still using a is our focal point. So the rate is still three fifths. It does not become two fifths for the Y value. Times negative three -7. Okay, that's 7 plus three over 5 times negative ten. And put that on your calculator to get Y equals one. So your point is 15 comma one. That's a choice. Again, if you like to graph it, that's perfectly fine. We'll give you some graph paper to do it on. Where you can get to 23. Number 9, triangle LMN Sean below. All right, we got some medians. That's important. Underlying it are drawn from point L and M to P and Q respectively. Segments MQ and LP intersect at R and Q, this whole median right here is 60. What's the measure of MR? Okay? So again, if we have the entire median guys, we should take this number, we should divide it by three, because we're going to split it up into thirds. Medians divide each other into a ratio of two to one. So that makes a total of three parts. Okay, so divided by three that gives you 20. Remember, if there's three parts MR is the long piece here, right? So it's the two of the two to one. So 20 times two is 40. This piece is 40 if they ask for QR, which they didn't. That would be 20. 20 and 48 up to the total of 60. So 40s are answered. Number ten, just different color here. And the diagram points E and D are the midpoints. Okay, so now we have midpoints. This is important here. Of sides AC and BC segments AD and BE intersect at F so BE is a median. AD is a median, right? Because they told me E and D are midpoints. So you have to identify that stuff. They're not just going to tell it to you, okay? Now identify what we have. AB is 28. AD, this entire length is 30, and BE, okay, BE is this entire length as well. I'm going to get ugly to write this. I'll try to make it. I'm just going to make it really big and go around the whole thing is 24. Okay? What's the perimeter of triangle DEF? So this small triangle in the middle. All right. Well, easiest one to find here is probably ED. ED is a midsegment. It's not a median. It's a midsegment because it connects to midpoints. Mid segments are always half of the side their opposite from. So this is 14. All right, we also need FD. Well, that's a part of the entire median AD, just like we did last problem divided by three, that gives you ten. Okay? So this small piece is ten. That'll make this piece 20, although they didn't even ask for it. And FE is a small piece of this median, take 24 divided by three and you get 8. So that's 8. Again, if they wanted this piece, it would be 16, just double the 8. And then add them up 14 plus ten plus 8, I believe, gives you 32. So because it said perimeter, right? 14 plus ten plus 8 is 32. Answer choice, right? Now, I want to stay on this question for just another minute. I want to talk about something. If they asked you for a similarity transformation to transform this triangle into triangle AFB. Similarity transformation. Here's what you would have to do. I think everybody would know the first step would be to rotate 180° around point F I think everyone would pretty much be all over that one. We wouldn't have too much of an issue there. Got a rotate it. Now the second one, remember, it's a similarity transformation you better have a dilation in there somewhere. And we definitely have to make FED bigger to match up with the other triangle. So we would dilate, now remember, when you dial it, you have to give the center of dilation. So I'm going to say with center, right now remember, if you rotate this, it's going to be looking like this a little bit. Here's E, here's D hopefully you see that your center of dilation should be F because you don't want it to move, so it's center at F, okay? And then you need a scale factor. And a scale factor. Of now think about it. These are medians, right? This is a two to one ratio. So again, if we want FD to match up perfectly with AF, we have to multiply it by two. So with a scale factor of two would be our answer here. All right? That might be something good to know. I don't know, maybe a good test question or something like that. Okay. Number 11, in the diagram of the right triangle, QRS, chambal, altitude. Here we go. Now they're telling us this is an altitude, okay? That's important. That should bring a bow in our heads. Is drawn from R to the hypotenuse of QS. So that means these are right angles. Okay, so there's that nice picture we like. If QT is 6, TS is ten, then what's the length of QR? All right, this is our tree question, okay? So you should turn your paper so that QS is on the bottom. All right? Remember guys, there's only three options for what your tree quote unquote can be. It can be this, and you can be there for it can be there. Okay? According to this question, I have no interest in RT or RS, so those aren't going to be my trees. All right, I noticed a lot of you want to make the altitude the tree every time that it's not the case. So I'm going to use my green marker here, there's my tree, QR, okay? Now, set up your proportion. Two fractions equal to each other. Remember top left and bottom right have to be the so called tree. Okay? Or tree is going to be QR here. So it's X X goes here, X goes there. The tree never goes on the same level. They go diagonal from each other. Now the tree can fold down. This is why we use a tree analogy, right? Can the tree fall down on top of the 6? Of course you can. So put a 6 down there. In the tree fall down on top of the ten, just the ten. No. When you cut down a tree, the root doesn't move over a bunch of feet and then fall, right? It just falls down. It can fall over the entire thing, though, so the entire thing is 16. So what we do, cross multiply and solve, get X squared equals the square root of 96. Now, all your answers are in simple radical form. So I'm going to go over how to do that. But if you're a little bit lost, you can just all right, so you could put that in the calculator and put these in the calculator, she was doing the same, but let's simplify it. 96 is divisible by 16, all right? Now, I know that because I did it beforehand, but you should check all your perfect squares, you know? And see which one works. 96 divided by 16 gives you 6. So let's break this up into radical 16, radical 6, square root of 16 is four. You keep the rad 6. There's your answer. You might have to test a couple before you find the one that works. Being 16. But you can also just throw this in the calculator, throw all of these in the calculator, see if it's one exactly the same. Number 12 is our first construction here. So we have segment AB shown along with point C using only a compass and straight edge dilate AB using a center of C and a scale factor of three. Okay. So we need a scale factor of three here. Let me get my compass out. Move this down. All right. So first thing we have to do, guys. The center is at C, we want to dilate AB. So you're going to take your straight edge, you're going to connect C through B they can make a nice long line, connect C through a, make a nice long line, and that should be beginning. Okay? It has to start that way. You don't want to connect B through a and extend it out or anything like that. Your center is C, you want to go from C take your compass, move it over to C and find the distance from C to B basically you're just copying a line segment three times. So Mark that angle. If you don't mark that angle, I don't know what you did, or that distance I should say. Now move up to point B Mark that off again. If the scale factor was two, you'd be done, right? Because you'd have one, two arcs. But the scale factor is three. So you just have to make one more. Right there. Okay, so you're done with that part. Now you just move the compass down to C and measure it off to point a. Make it work. Again, you need three tools. So one, move it over. Here's two. Put it over one more time. There's three. Okay? So again, if it asks for two, you do two. Fast for three, you do three. And you're going to connect these two to make an actual line segment. And then you're just going to label it appropriately. So this was B now it's B prime. This was a now it's a prime. Don't forget to label it. It asks you to label it as a prime B prime. Please do so. Okay, next up. This is a measure of angle CBA is 63°. So this angle right here, CBA 63, okay? What is the angle C, B prime a prime? So again, if you didn't label, you don't know what that is. But C to B prime to a prime is right here. What's this angle? Well, hopefully you're thinking, all we do is dilate something, so the angle is not going to change. So angle C, B prime, a prime equals 63°. I'm going to say dilations. Preserve angle measure. Preserve angle measure. Say whatever you dilate last time, you should all measure. Whatever you dilate, you're not going to change in angle. All right, next up, number 13. We have segment RS is the image of PQ after a dilation centered at an unknown point. Using only straight edge determine the center of dilation. So think about what we did last time. The first thing we did was we connected the center of dilation outwards, all right? Now, if we wanted to go backwards, couldn't we just connect a prime through a and B prime through B and they would meet at the center. So that's exactly what we're going to do here. So we're going to connect P back through R there you go. And we're going to connect Q back through S wherever the two lines meet with that was your center of dilation originally. It's just doing what we did backwards. So I have system market to see. Give one possible ratio of segment lengths that could be used for a dilation factor. Again, whenever we want to factor, we want new over old. All right, so let's see. RS is the image of PQ after a dilation. So PQ was the one that was being dilated. All right? So this segment was dilated right here. So the old was actually P to C this was the original. So that's going to go on the bottom PC. The new is RC. Because that's the image after the dilation. So that's one way you can do it. All right, you can also use the bottom, right? You could do SC that's the new part there over QS, which is the old. Okay, next up, interesting question, not one that we've really done before, but it does drive home a point that is important. Using a composite straight edge, so let me get my now again. There it is. Bring it down. Okay. Dilate AB using the center of C and a scale factor of .5. So we know if the scale factor is .5, that AB needs to get smaller. Leave all construction marks. So we haven't really done one like this, okay? But the important part I'm going to make this note here is that if the center center of dilation is on the line, then the line itself. Does not move. All right, so we've talked about that before. Like when we have a line and there's a center of dilation on it, the equation of that line stays exactly the same. Now, this is a line segment so it's going to get smaller, but same idea applies. All right, so again, if we want this to be half as big, then whatever the distance from a to C was, we want half of that the second time, whatever the distance from C to B was, we want half of that this time. Well, the only construction we know to find halfway between two points is a perpendicular bisector. So what I'm going to do that start today go as long as you want as long as it's farther than halfway. So I'm going to go there, mark up, mark down. Switch over to point C, keep your pen or pencil in the same circle. Arc up lock down. All right, then all you have to do is connect these two. And wherever they pass through the line, is your new point a prime. Now you have to do the same exact thing over here with BC. So measure from B anywhere as long as it's farther than halfway. That looks good to me. Arc up and down. Okay, flip on over to C do the same exact arc up and down. Okay, connect to two intersection points. Wherever they intersect the original line is the new B prime. So there's your new line a prime to B prime. Again, not terribly important, but the top part is if the center of dilation is on the line, then the line doesn't move. It might get shorter if it's a segment, but the line itself doesn't move. Next up, in the graph shown below. B prime B prime is the image of AB after dilation, so this is the new. This is the old. What is the value of the dilation scale factor? So we need to find a scale factor. So again, we need to do new overall. Now, you could do the distance for you for a prime B prime and AB and divide them, but that's kind of a nightmare. All right, so here's what I would do. Just take either the vertical distance or the horizontal distance. It doesn't matter what you do. Okay? The old would be this distance from a to the origin, so it's a distance of one, two, three, four, 5, 6, 7, 8. The new would be this entire distance, which is 8, 9, ten, 11, 12. Okay? So you can just do 12 over 8, which simplified down is three over two. And that's it. You could also have done the horizontal distance to the bottom, right? The bottom is one, two, three, four, 5, 6, 7, 8, 9, ten. And 11, 12, 13, 14, 15. So ten and 15, you could have done the newest 15 over the oldest ten and gotten 1.5, which is three over two. I don't know why I wrote this 1.5, but the same thing. If you wrote 12 hour rate is 1.5, it would have worked as well. All right, moving on, 16. Align with an equation Y equals two X plus three is dilated with the center of dilation at the origin. We like to see that the center is at the origin that makes our life easy. Scale factor is 6. So it's getting 6 times as big. Ava believes the equation will be Y equals 12 X plus 18, Serena believes the equation is two X plus 18 is one of them correct. If so, why? Okay? So one of them is definitely correct. So remember, whenever we do dilations, so I'm going to make another note dilations means slope doesn't change. Okay, again, just like angles don't change, neither does a slope of a line. So Ava can't be right, she took the two and multiplied the slope by 6 to get 12. Can't do that, okay? Serena kept the slope exactly the same as two, but multiplied the Y intercept by 6, and that's correct. Okay? So Serena's correct. Slope stays the same. Slope stays the same. But the Y intercept gets multiplied. By the scale. Oops, that's terrible and ready. Scale factor. Okay, that's it. Moving on. The line whose equation is Y equals one half X minus three is dilated by a factor of three. The center at this point. So that's not the origin anymore. Since explain why its equation would not change, okay? Guys, if the equation of the line doesn't change after dilation, there's only one reason for that. That reason must be that ten comma two lies on that line. Okay, so I'm just going to write that right away. That's the only viable option. Ten comma two lies on the line. One half X minus three. That's your answer, okay? Now if you want to show why that works, well let's plug in ten for X two for Y so you get two equals one half times ten minus three. And that's two equals one half times ten is 5. Minus three and obviously two is two. So ten comma two lies on the line already. The equation of the line won't change. 18 in the diagram below AE and BD intersect at C with segments segment lengths marked as shown. Describe a similarity transformation. That would map CDE that triangle onto CBA. Give as much detail as possible. So first off, okay, to get this triangle over here, hopefully we also have to rotate it. Not a reflection, right? A reflection would make it look something like that. But we want to rotate it. Okay, so I'm going to say rho T and remember you have to say how many degrees, 180°. If it's one 80, you don't have to say clockwise or counterclockwise. It doesn't make a difference. And you have to say the point. So around or about C okay, there are step one. Step two, it's a similarity dilation again. I mean, similarity transformation, you better dilate. So you have to find the scale factor. So I'm going to say SF for scale factor. Well, new over old, again, the new is going to be the bigger triangle. So take one of the bigger sides it doesn't matter. Let's say 15. Divided by its corresponding older side. Well, its corresponding older side is its 9 right here. You could have also done ten divided by 6 and would have given you the same thing. That's just new overall. So 15 divided by 9, simplify that. They can both be divided by three to make this 5 over three. So there you go. We have everything we need. So dilate, you have to give the center. With center at 70, hopefully we don't want C to move, right? So we know that that has to be the center. And scale factor, I'm going to abbreviate in the interest of time and scale factor of 5 over three. Okay. Last part here, if DE is equal to 5, find the length of AB to the nearest tenth. All right, well, I already know the scale factor, right guys? So I can just take 5 and multiply it by the scale factor 5 thirds, okay? If you put that in the calculator, you get 8.3 repeating. It asks you to round to the nearest tenth, so that's just 8.3. Okay? If you didn't want to use the scale factor, you could have set up a proportion, right? You could have set up 15 over 9. Those two sides correspond to each other equal X over 5. Then you would get what, 9 X equals 5 times 15 is what, 75? Divide them both by 9. And again, you're going to get X equals 8.3 repeating. Which rounded is 8.3. So either way you get the same thing. But if you already know the scale factor, guys, it's easy enough to just multiply the scale factor by the side length. All right, almost there, number 19. So we got in the diagram shown below BD. It is parallel to CE. AB is four BC 6 AC is X plus three. AC is X plus three. This is a D I'm sorry. A D is X plus three. My band DE is two X plus one, all right? The term the value of X all right, so take a look at what we got here. This nicely enough is size player theorem. Okay, we're allowed to use side splitter for this, which is really awesome. It makes our life easy. Why? We got these two parallels here so the triangles are similar. We have the opposite sides. And neither one of these are on the parallels. Like we had before. So set up your size player theorem. You can just do four over 6. Equals X plus three over two X plus one. And there are other things you can do, all right? You can also do four over X plus three equals 6 over two X plus one, right? All those things will work. Now when you cross multiply be careful, you actually have to distribute each number. So I'm going to write it out the long way so we see it. That's what you're really doing. So distribute the four. You get 8 X plus four, and you get 6 X plus 18. All right, move the 6 X over. Let's go here. We got two X plus four. Equals 18. Subtract the four off of both sides. You get two X equals 14. And divide by two, you get X equals 7. So there's your value of X right there. Okay? Next part CE these different color is 30. We want to know the length of BD. So here's the example where you can't use side splitter, right? Because we're looking for the parallels. Or we're given the parallels. But you can set up a nice proportion. Four and X are both part of triangle ABD. So you can do four over X if you want. Equals. Now 30 is a part of the big triangle ACE. So if you want the big triangle, you need all of HC that's ten over 30. All right, simplify and solve cross multiply, you get one 20, equals ten X, divide by ten, and you're going to get X equals 12. And that's the length. So understand when you can use side splitter and when you can not, that will be helpful. Okay, here we go. Line segment a, B has endpoints at negative four negative one. I'm going to plot that. And 8 comma 7, that's up here. All right, so here's a here's B, I'm going to connect these nicely this time to make my life a little bit easier. Okay. And let's see what they want. Point Q lies somewhere on AB such that we have this proportion. Awesome. So we know how to do these for giving a nice graph this time. So we can do a graphically. So create your right triangle. I'm going to do that. I'll use a different color. I'll continue using the green here. So there's the vertical, here's the horizontal for my right triangle. All right. And we just have to count boxes now, right? So from a over to the bottom right, we have one, two, three, four, 5, 6, 7, 8, 9, ten, 11, 12 boxes. And up and down, we have one, two, three, four, 5, 6, 7, 8 boxes. Okay? We like to see those numbers 12 and 8, right? Because the three to one ratio tells us we're breaking into four parts. 12 and 8 are both divisible by four. It's going to make it easy. So if you want, you could say AQ is three fourths of the whole thing. And BQ is just one fourth of the whole thing. And you can use a or you can use B it doesn't matter. But first we got to break it up. So if I want to break 12 up into fourths, then I need to go every three boxes because 12 divided by four is three. So I'm going to go one, two, three, break it up one, two, three, two, three, one, two, three, good. And make sure you have four segments. One, two, three, four. All right, 8, again, 8 divided by four. It's two, so I'm going to go every two boxes. One, two, two, one, two, one, two. Make sure you have four segments. I do. Now, I'm going to go from a, a is three of the fourths, so count from a one, two, three sections. All right? This is going to be my vertical piece. Again, I'm going to continue to use a since a is on the bottom. I'm going to count from the bottom one, two, three. See where they connect right there is going to be my point. Q right? So Q is at point what's just 5 comma 5. It is 5 comma 5. You don't really need the equals there, but if you want it. Next part, what is the ratio of a Q to the length of AB? Okay, so we want the ratio, a Q to a, B well, think about it. We already said AQ is three fourths of the whole thing. That means that AB is the whole thing, or four fourths, which is weird to think about, but it works. So 8 Q to AB is just a four to three ratio. If you wanted to, you can take the distance formula for AQ and AB and find the ratio from there. But that's enough. Just to do four to three. All right, last question. A wooden structure has the shape in the form of a right triangle. So look at my diagram already. This already looks like a diagram we can use our trees for. Or hills or sass, if you like to use that. Since the basis 12 feet and the height is 8, it's supported by a wire stretched from sea to the ground. So there's no support wire. At that point, okay? To support wires perpendicular, they already drew that for us. How far away from point B should point DB place. So I want to know this right here. Again, you only have three options for your tree. One, two, three. I don't care about AC, right? I don't care about CT, but I do know something about CB, so that's the one I care about. So again, this one happens to be the altitude, the piece in the middle. It's not always. And also, my tree here, here's my tree, okay? Is not going to be X it's not always X guys. It is sometimes, but it doesn't have to be. So my tree again goes top left, bottom right, 8 and 8. If the tree's in the middle, it can fall to the left, right? That would be 12. It can also fall to the right. That would be X so this is an easier one, actually, cross multiply itself. 8 and 8, 64, equals 12 X, divide by 12, and you get around to the nearest tenth. When you round it, you get X equals 5.3, if you round it properly. All right, next piece says it to the nearest tenth of a foot, how long is your support wire? Okay, so now I need a new tree, right? I'm going to call my support wire. I already used X here. So I'm going to call it Y all right? Now, here's the bottom. Here's the bottom, which is X, which I now know, I should really rewrite this as 5.3. Okay? The support wire is going to be my tree. Why? Because I now care about the support wire, right? I don't care about this line in the middle. I just care about the support wire. So set up your proportion, okay? To support wire is going to be my tree. So that means I'm going to have Y and Y in the top left bottom right. Now can the support wire fall down on top of X, which is 5.3? Yes. Can this support wire fold down on top of 12 solely 12? No. This can't all of a sudden jump over here and then fold down. That doesn't make sense. Trees don't do that. That's why we use the tree analogy. But this can fall straight down and fall on both of them, right? So find the total. 12 plus 5.3 is 17.3. So use that 17.3. Okay, cross multiply and solve. Y squared equals you get 91.69. Take the square root and remember you're in rounding to the nearest tenth, so you get Y equals 9.57, which rounded is 9.6. Feet. And there's your final answer. So two questions with the same diagram, but using different sides as quote unquote trees. All right, so hopefully this was helpful. Okay guys, study, make sure you know different things medians, altitude, all right, ratios, new over old, okay? Scale factor dilation, all that good stuff. All right, please come see whoever your teacher is for extra help. And good luck.