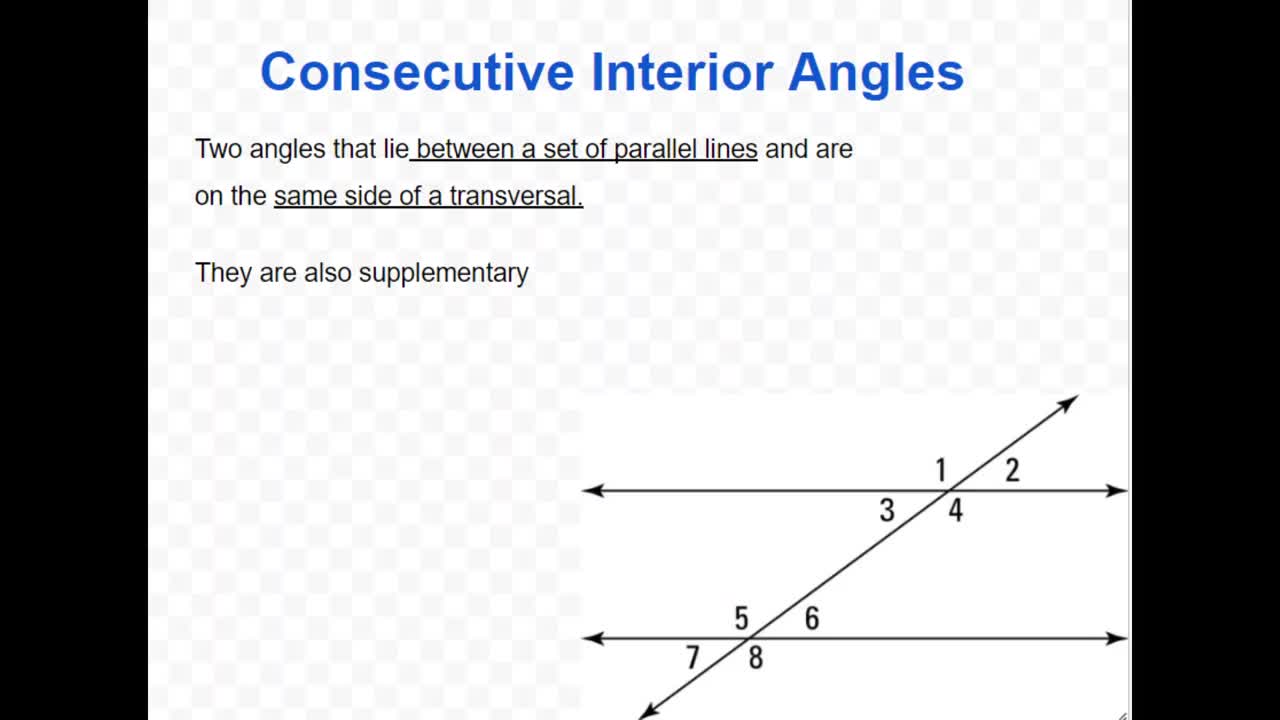
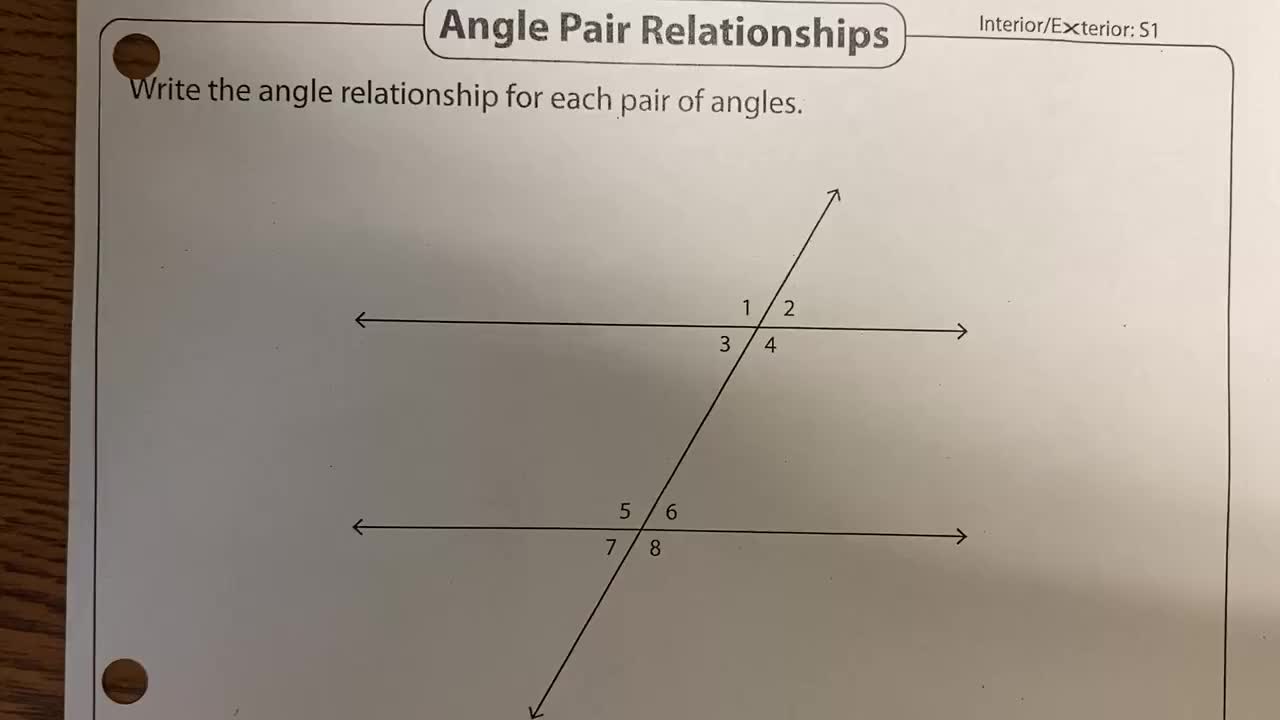
Circle Angles and Arcs
Middle School / Math / Geometry
Four problems involving circle arcs and angles
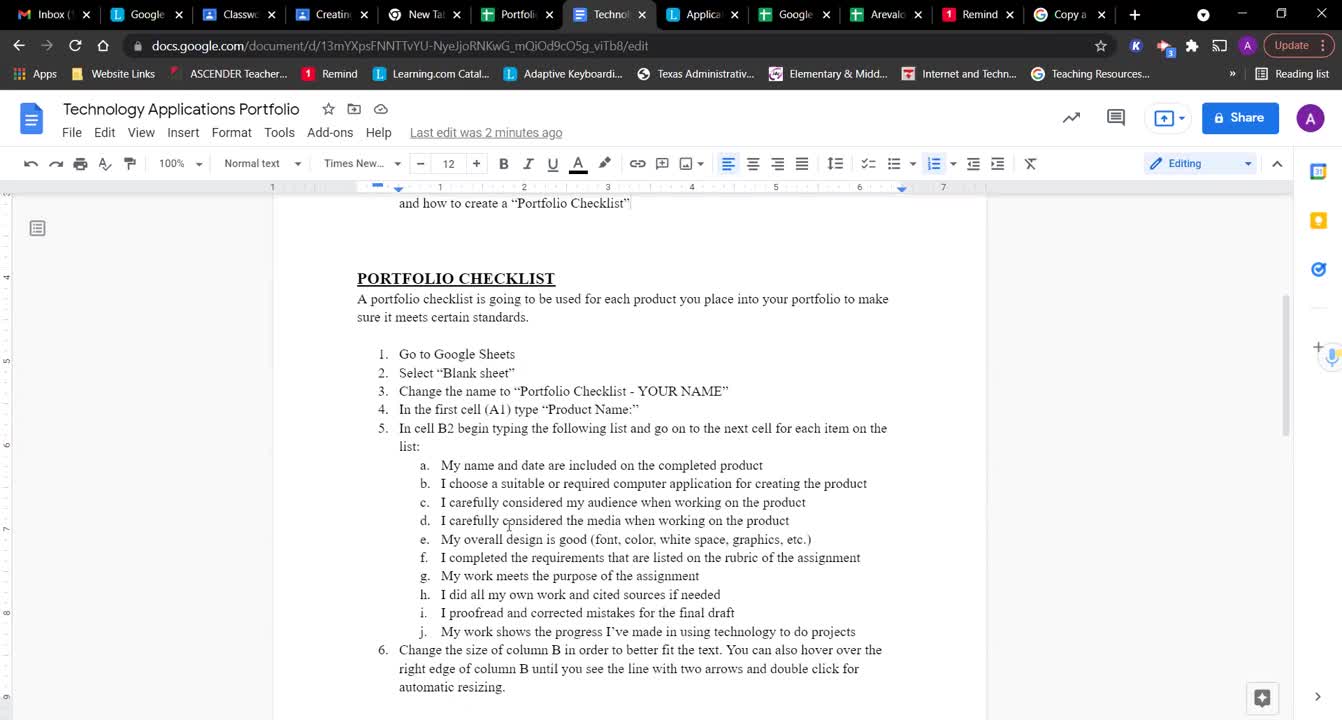
Okay. This problem here for you to check your work on is asking you to find the measure of angle TSV. The middle letter there, the S, tells us that?s the full angle. The T is where we?re starting. The side the we are starting. And the V is the side that we are ending. So, if we trace this angle path, this should be TSV. The angle we?re looking for is essentially that angle. S is the center of this circle so that makes angle TSU and angle USV central angles which also makes angle TSV central angles.
Now the measure of a central angle, just recall from the other day, is equal to the measure, oh gosh math teacher not a speller, of the included arc. So, the arc that?s contained between the two legs. So, on this question we are actually not even having to look for the arc so I just wanna remind you of that so remember this, Oh gosh, I spell really, really bad, I?m sorry. Remember me. Sorry. Okay. All this one?s really asking you to do is detect the angle TSU and the angle USV so basically this is going to be the measure of TSU plus the measure of USV and that?s gonna give us TSV. So, this would be sixty-five degrees plus sixty degrees equals a hundred and twenty-five degrees. So that?s how you do the first one.
Second one. Second one is an inscribed angle. So, the thing you wanna know on an inscribed angles that will help us, and we have to use the rule of an inscribed angle says measure of an inscribed angle is equal to half the measure of the contained arc. So, the arc that is in that angle is half the measurement of the inscribed angle.
So, this one here we kinda need to look at what we?re given. They?re given me a ninety-four degrees right here, I see my question mark is at F, and they?re given me this right here, line HF from yesterday?s lesson or from previous lesson, so you would say line segment HF is a diameter of the circle. What does the diameter mean? It cuts the circle in half. So, if that?s the case, then measure of HWF?s arc equals one hundred eighty degrees because we know half a circle is one hundred eighty degrees. These are key fact that you need to know. Well, if we know this entire arc is a hundred eighty degrees, and we know right here that little segment there is ninety-four degrees, I can figure out the measure of arc HW. So, if I say one hundred eighty degrees minus ninety-four degrees, that?s gonna give me the measure of that arc. Okay? So, you can do this and Okay and that?s gonna give you eighty-six degrees. So, if we look back up here at my beautiful circle, I?m gonna take this highlight off just so we can see a bit clearer, the measure of this arc is eighty-six degrees. So, if this is eighty-six and this is ninety-four what does that mean about the question mark? Well, if you look at the question mark you see I?ve already highlighted the diameter in blue. If I take that diameter and connect cord FW or WF were gonna make an inscribed angle which is a measure of that question mark. Now if you look, that inscribed angle also contains the value of the arc we just found of eighty-six. So, by our inscribed angle rules, the degree of the question mark is gonna be half the measure of the arc. So, we are gonna say the measure, what angle is that, HFW is the question mark, remember put your vertex of your angle in the middle, equals one half times eighty-six is forty-three degrees. So, the measure of question mark is forty-three degrees.
So, the next one, let?s check our work on this one. This one is asking for the measure of the arc. Now, this is showing me that we have a diameter RT. And we also have a central angle here at RST of forty degrees. What we?re looking for [is] the arc of TRS. So, TRS is T, R, S, it?s the purple. Well, if RT is a diameter then the measure of arc TR is a hundred and eighty degrees. Now, the measure of arc RS they give me is forty degrees. So, all you have to do? Add ?em. So, I have two hundred and twenty degrees is the measure of arc TRS. That?s all you do on that one. Good job. And that is of central angle.
Alright! This one here is another inscribed [angle]. How can I tell the difference between ones that are inscribed and ones that are central? Inscribed angle?s vertex is not in the center of the circle. Where if you look at the previous one you saw how the vertex was in the center of the circle. On the first one the vertex is in the center of the circle. But on the second problem and on the fourth problem the vertex is not. Its on the outside of the circle. That there tells us that these are inscribed angles and not central angles.
So, we got this central angle and we got to find x. So, again our center angle thing says that the measure of angle MNL equals one half the measure of arc ML. That?s what our rule tells us. So, I?m gonna say measure on MNL, which is the only angle given on this one. It?s this one right here. The measure of that angle which is six x minus four is gonna equal one half the measure of the arc, which is seventy-six. So, what you?re gonna do now is you just have a multistep equation. So, I?m gonna say six x subtract four equals thirty-eight coz seventy-six divided by two is thirty-eight. I?m just gonna solve this out so I?m gonna add my four. So, I?m gonna get six x equals forty-two. Now, I?m gonna divide both sides by the coefficient of x which happens to be six in this case. So, x equals seven. And that?s all you do. Hope this helps. Good luck trying these.
Now the measure of a central angle, just recall from the other day, is equal to the measure, oh gosh math teacher not a speller, of the included arc. So, the arc that?s contained between the two legs. So, on this question we are actually not even having to look for the arc so I just wanna remind you of that so remember this, Oh gosh, I spell really, really bad, I?m sorry. Remember me. Sorry. Okay. All this one?s really asking you to do is detect the angle TSU and the angle USV so basically this is going to be the measure of TSU plus the measure of USV and that?s gonna give us TSV. So, this would be sixty-five degrees plus sixty degrees equals a hundred and twenty-five degrees. So that?s how you do the first one.
Second one. Second one is an inscribed angle. So, the thing you wanna know on an inscribed angles that will help us, and we have to use the rule of an inscribed angle says measure of an inscribed angle is equal to half the measure of the contained arc. So, the arc that is in that angle is half the measurement of the inscribed angle.
So, this one here we kinda need to look at what we?re given. They?re given me a ninety-four degrees right here, I see my question mark is at F, and they?re given me this right here, line HF from yesterday?s lesson or from previous lesson, so you would say line segment HF is a diameter of the circle. What does the diameter mean? It cuts the circle in half. So, if that?s the case, then measure of HWF?s arc equals one hundred eighty degrees because we know half a circle is one hundred eighty degrees. These are key fact that you need to know. Well, if we know this entire arc is a hundred eighty degrees, and we know right here that little segment there is ninety-four degrees, I can figure out the measure of arc HW. So, if I say one hundred eighty degrees minus ninety-four degrees, that?s gonna give me the measure of that arc. Okay? So, you can do this and Okay and that?s gonna give you eighty-six degrees. So, if we look back up here at my beautiful circle, I?m gonna take this highlight off just so we can see a bit clearer, the measure of this arc is eighty-six degrees. So, if this is eighty-six and this is ninety-four what does that mean about the question mark? Well, if you look at the question mark you see I?ve already highlighted the diameter in blue. If I take that diameter and connect cord FW or WF were gonna make an inscribed angle which is a measure of that question mark. Now if you look, that inscribed angle also contains the value of the arc we just found of eighty-six. So, by our inscribed angle rules, the degree of the question mark is gonna be half the measure of the arc. So, we are gonna say the measure, what angle is that, HFW is the question mark, remember put your vertex of your angle in the middle, equals one half times eighty-six is forty-three degrees. So, the measure of question mark is forty-three degrees.
So, the next one, let?s check our work on this one. This one is asking for the measure of the arc. Now, this is showing me that we have a diameter RT. And we also have a central angle here at RST of forty degrees. What we?re looking for [is] the arc of TRS. So, TRS is T, R, S, it?s the purple. Well, if RT is a diameter then the measure of arc TR is a hundred and eighty degrees. Now, the measure of arc RS they give me is forty degrees. So, all you have to do? Add ?em. So, I have two hundred and twenty degrees is the measure of arc TRS. That?s all you do on that one. Good job. And that is of central angle.
Alright! This one here is another inscribed [angle]. How can I tell the difference between ones that are inscribed and ones that are central? Inscribed angle?s vertex is not in the center of the circle. Where if you look at the previous one you saw how the vertex was in the center of the circle. On the first one the vertex is in the center of the circle. But on the second problem and on the fourth problem the vertex is not. Its on the outside of the circle. That there tells us that these are inscribed angles and not central angles.
So, we got this central angle and we got to find x. So, again our center angle thing says that the measure of angle MNL equals one half the measure of arc ML. That?s what our rule tells us. So, I?m gonna say measure on MNL, which is the only angle given on this one. It?s this one right here. The measure of that angle which is six x minus four is gonna equal one half the measure of the arc, which is seventy-six. So, what you?re gonna do now is you just have a multistep equation. So, I?m gonna say six x subtract four equals thirty-eight coz seventy-six divided by two is thirty-eight. I?m just gonna solve this out so I?m gonna add my four. So, I?m gonna get six x equals forty-two. Now, I?m gonna divide both sides by the coefficient of x which happens to be six in this case. So, x equals seven. And that?s all you do. Hope this helps. Good luck trying these.